Someone on the Ducati Index mentioned that he would like to put a 916 into a 907ie chassis, because the 916 makes more torque than a 907.

Following are a couple charts on the subject.

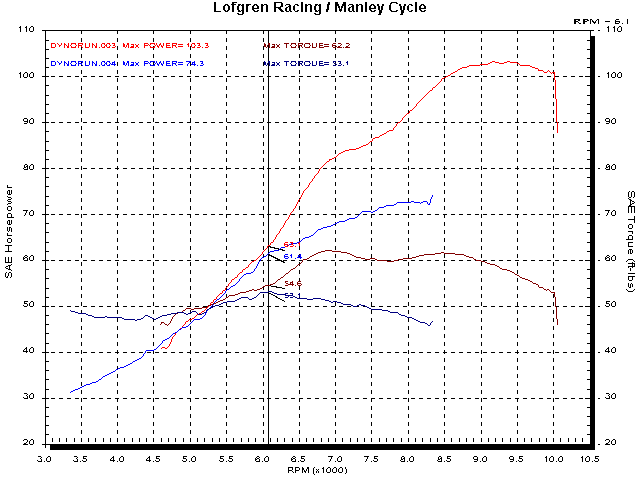
First, a stock 916 (red-HP, brown-torque) and a stock 907ie. Below 6100 RPM there isn't much difference, but the 916 run doesn't even start below 4500 RPM.

The 916 does make 17% more torque than the 907 above 6100 RPM.

Below is a chart of the same two bikes. (916, green - baseline, blue - tuned and 944cc 907ie post big bore, porting, tuning.) 

Notice that both 'tuned' bikes have the same peak torque. The 907ie needs 24 more ccs and a little more compression as well as increased port efficiency (porting) to equal the torque of the 916 (thank you valve area! 1710 square mms, vs 1520 square mms), but that makes them pretty close in displacement-specific-torque.

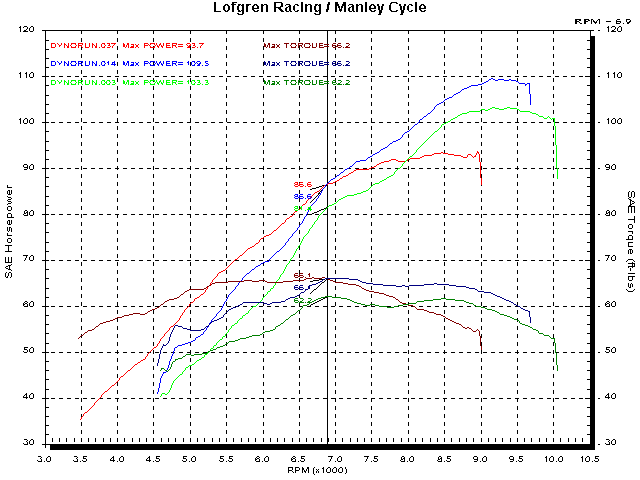
The question is; do you want it above or below 6900 RPM?

But, y'know, I'm not sure it really matters, 'cause the front wheel will probably hit the 916 head.

One other thing. You really want the power. It's not an 'either-or' thing, you can't make power without making torque.

Following is an article about this very subject.

I wrote this for Minnesota Motorcycle Monthly in the spring of 2002

That Torque vs Horsepower Thing

A couple weeks ago a customer asked that we tune his Buell for torque.

That’s difficult because an engines potential is set by the components and specifications with which it is assembled. You can squander that potential by not getting the ‘tune’ correct (air/fuel ratio and ignition timing) but you can’t get any more without adjusting the parts or specs.

(With a fixed maximum ignition timing (points or non-digital electronic ignition system) the WOT power may be biased toward the torque peak or the power peak but that is typically on the order of a couple percent over a few degrees of timing variation.)

An engines volumetric efficiency is represented by the torque curve. (Not exactly, but close.)

Specific Torque of torque-per-liter is an indication of an engines efficiency.

The chassis responds to torque. The degree of pro or anti-squat of the rear suspension is a product of torque, (this is modified by gearing) and the chassis attitude (ie, wheelie) is a result of increase in torque. (A rapid increase in torque, either opening the throttle, ‘fanning’ the clutch, or a big rise in the torque curve can cause a wheelie.)

It is fairly well known that the maximum acceleration, in each gear, occurs at the torque peak. However, this fact is often misunderstood. The important aspect is the ‘in each gear’ part.

A tuner needs to know about the torque characteristics for several reasons mentioned above, but from a performance standpoint (that would be the work!!)  power is what counts.

Let’s take a look at the power and torque of a 750cc Ducati in 3^rd and 4^th gear.

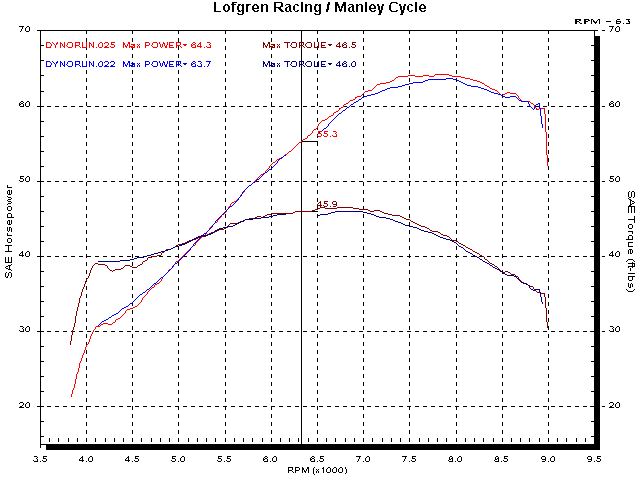
Below is a chart of 3^rd (blue) and 4^th (red) gear power curves plotted against speed. That is a realistic situation. At 78 MPH the power in 3^rd gear is 63.7 HP and the power in 4^th gear is 55.3 HP.

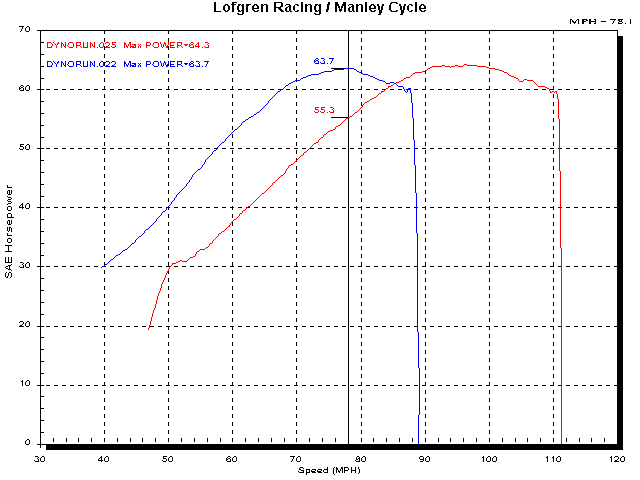
Next we look at the power and torque of both tests plotted against RPM. Remember that the torque values are calculated to be ‘at the crank’ and do not represent the torque around the rear axle.

Also, note that the power values are slightly different for 3^rd and 4^th gear. Since the engine/drive-train is accelerating during these tests (they are performed on a Dynojet inertia type dynamometer) and it is accelerating faster in 3^rd gear than in 4^th gear, slightly more energy is stored in the drive-train is 3^rd vs 4^th gear. (This 1% difference will be applied at the end if this article.)

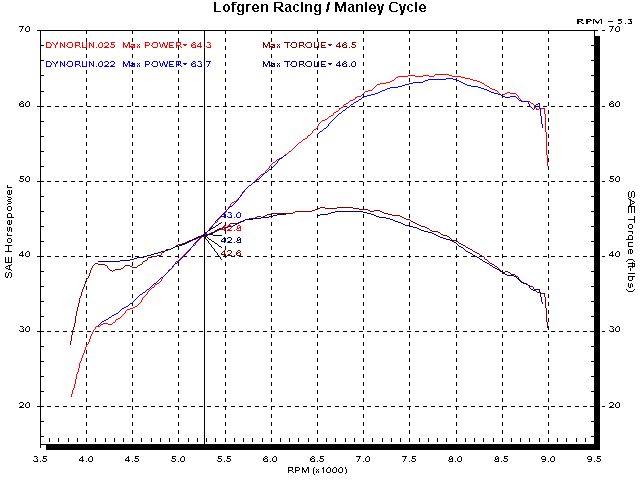
In 3^rd gear at the same speed as the chart above, the power is 63.7 HP and the torque ‘at the crank’ is 42.2 lb ft.

Below is the same chart with the cursor at 55.3 HP in 4^th gear. The torque ‘at the crank’ is 45.9 lb ft.

There is more than one way to explain this. I’m going to use the rear wheel power and torque, first.

The equation for calculating power from torque and RPM is; torque (in pounds-feet) times RPM divided by 5252.

Since the rear wheel RPM is constant at one road speed, the torque around the rear axle has to be proportional to any difference in power.

That means that the difference in rear wheel torque between 3^rd and 4^th gear is 63.7 (HP in 3^rd) divided by 55.3 (HP in 4^th). The torque at the rear axle is 115% higher in 3^rd gear than in 4^th.

Now look at it from the transmission and torque multiplication standpoint.

Since the rear drive and primary ratios remain constant we only need to look at the ratio difference of the 3^rd and 4^th transmission ratios.

The torque multiplication of 3^rd gear is 1.3333, the input gear has 24 teeth and the output has 32 teeth.

The torque multiplication of 4^th gear is 1.07407, the input gear has 27 teeth and the output has 29 teeth.

Multiply the torque ‘at the crank’ in 3^rd gear by the torque multiplication ratio of 3^rd gear.

That’s 42.2 lb-ft times 1.3333 = 56.26

Do the same for 4^th gear.

That’s 45.9 lb-ft times 1.07407 = 49.3

The resultant difference in torque between the two gears is 114.131%.

Multiply that by the difference in the measured power (1.0094 below the first chart) and there is your 115% difference at the rear axle.

Calculated both ways, the torque around the rear axle is higher with higher power.

Power is the measure of work, so it’s no surprise that higher power nets better performance. It’s the power that counts!